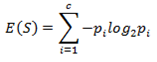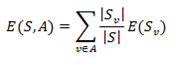| Map > Data
Science > Explaining the Past
> Data Exploration > Univariate
Analysis > Binning > Supervised |
|
|
|
|
|
|
Supervised Binning
|
|
|
| Supervised binning methods transform numerical variables
into categorical
counterparts and refer to the target (class) information when selecting discretization cut
points. Entropy-based binning is an
example of a supervised binning method. |
|
|
|
|
|
|
Entropy-based Binning
|
|
|
|
Entropy based method uses a split approach. The entropy (or the information content) is calculated
based on the class label. Intuitively, it finds the best split so that the bins are as pure as
possible that is the majority of the values in a bin correspond to have the same class label. Formally, it is characterized by finding the split with the maximal information gain.
|
|
|
|
|
|
|
|
Example:
|
|
|
|
Discretize the temperature variable using
entropy-based binning algorithm.
|
|
|
|
|
|
|
|
Step 1: Calculate "Entropy" for the target.
|
|
|
|
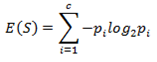
|
|
|
|
|
|
|
|
|
|
|
|
E (Failure) = E(7, 17) = E(0.29, .71) = -0.29 x log2(0.29)
- 0.71 x log2(0.71) = 0.871
|
|
|
|
|
|
|
|
Step 2: Calculate
"Entropy" for the target given a bin.
|
|
|
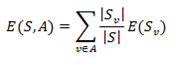
|
|
|
|
O-Ring
Failure |
| Y |
N |
| Temperature |
<= 60 |
3 |
0 |
| >
60 |
4 |
17 |
|
|
|
|
|
|
|
|
E (Failure,Temperature) = P(<=60) x E(3,0) +
P(>60) x E(4,17) = 3/24 x 0 + 21/24 x 0.7= 0.615
|
|
|
|
|
|
|
|
Step 3: Calculate
"Information Gain" given a bin.
|
|
|
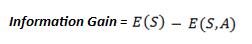
|
|
|
|
Information Gain (Failure, Temperature) = 0.256
|
|
|
|
|
|
|
|
The information gains for all three
bins show that the best interval for
"Temperature" is (<=60, >60) because it returns the
highest gain.
|
|
|
|

|
|
|
|
|
|
|
|
Exercise
|
|
|
|
|
|
|