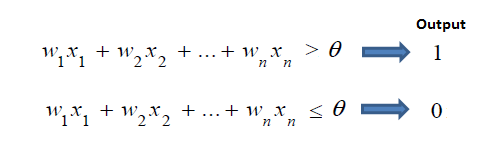| Map
> Data Science > Predicting the Future >
Modeling > Classification/Regression
> Artificial Neural Network >
Perceptron |
|
|
|
|
|
|
Artificial
Neural Network - Perceptron
|
|
|
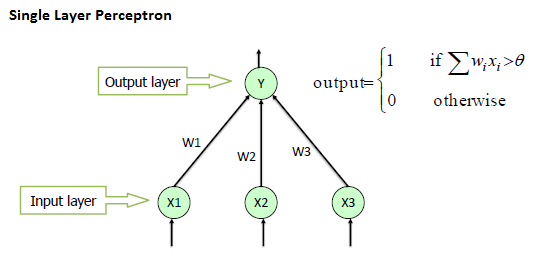
| A single layer perceptron (SLP) is
a feed-forward network based on a threshold transfer function. SLP is the
simplest type of artificial neural networks and can only classify linearly separable
cases with
a binary target (1 , 0). |
|
|
| |
|
|
|
|
|
|
| Algorithm |
|
|
| The single layer perceptron
does not have a priori knowledge, so the initial weights are assigned randomly.
SLP sums all the weighted inputs and if the sum is above the threshold (some predetermined value),
SLP is said to be activated (output=1). |
|
|
|
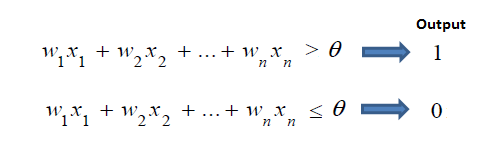
|
|
|
| The input values are presented to the perceptron, and if the
predicted output is the same as the desired output, then the performance is considered satisfactory and no changes to the weights are made. However, if the output does not match the desired output, then the weights need to be changed to reduce the error. |
|
|
|

|
|
|
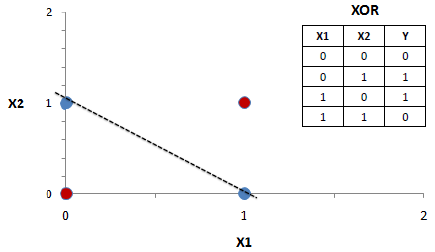
| Because SLP is a linear classifier and if the cases
are not linearly separable the learning process will never reach a point
where all the cases are classified properly. The most famous example of the inability
of perceptron to solve problems with linearly non-separable cases is the
XOR problem. |
|
|
|
|
|
|
| However, a multi-layer perceptron using the
backpropagation algorithm can successfully classify the XOR data. |
|
|
| |
|
|
| Multi-layer Perceptron - Backpropagation
algorithm |
|
|
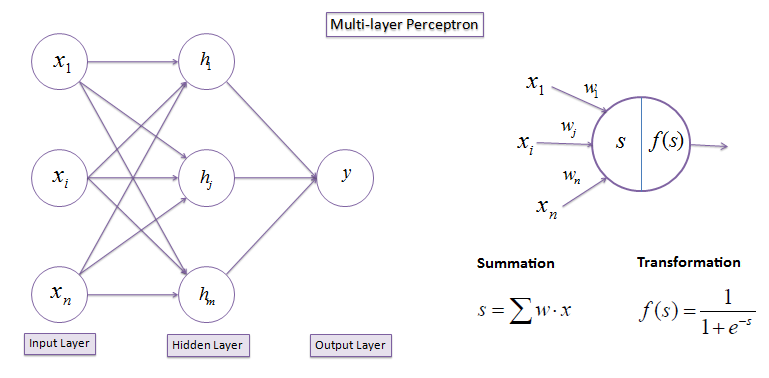
| A multi-layer perceptron (MLP) has the same
structure of a single layer perceptron with one or more hidden layers. The backpropagation algorithm consists of two phases: the forward phase where the activations are propagated from the input to the output layer, and the backward phase, where the error between the observed actual and the requested nominal value in the output layer is propagated backwards in order to modify the weights and bias values. |
|
|
| |
|
|
| Forward propagation: |
|
|
| Propagate inputs by adding all the weighted inputs
and then computing outputs using sigmoid threshold. |
|
|
|
|
|
|
| Backward propagation: |
|
|
| Propagates the errors backward by apportioning them to each unit according to the amount of this error the unit is
responsible for. |
|
|
|

|
|
|
| Example: |
|
|
| A Neural Network in 11 lines of Python |
|
|
| |
|
|
| ANN
Interactive (only Windows)
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|